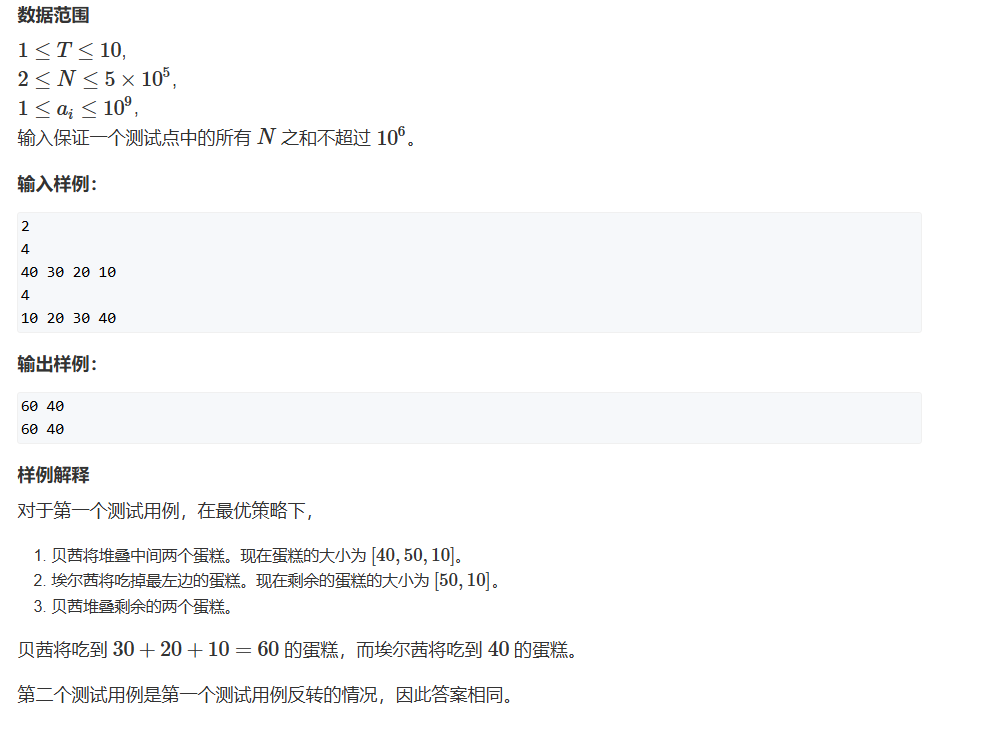
题目:

博主解题思路:
整体思路:
本题是一个关于两头奶牛分蛋糕的博弈问题,关键在于分析在双方都采取最优策略的情况下,如何计算出贝茜和埃尔茜最终吃到的蛋糕量。由于贝茜先行动(堆叠相邻蛋糕),埃尔茜后行动(选择最左或最右蛋糕藏起来),且最终贝茜吃剩下的一个蛋糕,埃尔茜吃藏起来的蛋糕,所以核心是找出埃尔茜能藏起来的最大蛋糕量,再用蛋糕总量减去埃尔茜的量,即可得到贝茜的量。
具体步骤
- 处理多组测试用例
首先读取测试用例的数量 T,然后对每个测试用例进行处理。对于每个测试用例,先读取蛋糕的数量 N。
- 计算前缀和
- 使用前缀和数组
s 来方便计算区间内蛋糕的总量。前缀和数组 s[i] 表示前 i 个蛋糕的大小之和。通过遍历输入的蛋糕大小数组,计算出前缀和数组:
1
2
3
4
|
long[] s = new long[n + 1];
String[] split = br.readLine().split(" ");
for (int i = 1; i <= n; i++)
s[i] = Long.parseLong(split[i - 1]) + s[i - 1];
|
- 确定埃尔茜藏蛋糕的次数
每一轮埃尔茜藏一个蛋糕,最终只剩下一个蛋糕给贝茜吃,所以埃尔茜藏蛋糕的次数为 (n - 1) / 2,记为 eTotal。
- 找出埃尔茜能藏起来的最大蛋糕量
埃尔茜藏蛋糕的过程可以看作是从蛋糕序列的左右两端选取一些连续的蛋糕。我们通过枚举不同的组合,找出能使埃尔茜藏起来的蛋糕总量最大的情况。具体做法是,枚举从左边选取 i 个蛋糕,从右边选取 eTotal - i 个蛋糕的所有可能组合,计算这些组合的蛋糕总量,并取最大值作为埃尔茜能藏起来的最大蛋糕量 e:
1
2
3
4
|
int eTotal = n - 1 >> 1;
long e = 0;
for (int i = 0; i <= eTotal; i++)
e = Math.max(e, s[i] + (s[n] - s[n - eTotal + i]));
|
- 计算贝茜吃到的蛋糕量
用所有蛋糕的总量 s[n] 减去埃尔茜藏起来的最大蛋糕量 e,即可得到贝茜吃到的蛋糕量 b:
- 输出结果
对于每个测试用例,输出贝茜和埃尔茜分别吃到的蛋糕量 b 和 e。
总结
通过上述步骤,我们利用前缀和数组来高效计算区间内蛋糕的总量,通过枚举不同的左右两端蛋糕组合,找出埃尔茜能藏起来的最大蛋糕量,进而计算出贝茜吃到的蛋糕量,从而解决了该博弈问题。
答案:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
|
import java.io.*;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int t = Integer.parseInt(br.readLine());
while (t-- != 0) {
int n = Integer.parseInt(br.readLine());
long[] s = new long[n + 1];
String[] split = br.readLine().split(" ");
for (int i = 1; i <= n; i++)
s[i] = Long.parseLong(split[i - 1]) + s[i - 1];
int eTotal = n - 1 >> 1;
long e = 0;
for (int i = 0; i <= eTotal; i++)
e = Math.max(e, s[i] + (s[n] - s[n - eTotal + i]));
long b = s[n] - e;
bw.write(b + " " + e);
bw.newLine();
}
br.close();
bw.close();
}
}
|