求整数的因子(也称为 约数)可以使用 从 1 到 √N 迭代的方法,这样可以大幅减少计算次数,从 O(N) 优化到 O(√N),大幅提升速度。
1. O(√N) 高效因子枚举
原理:
- 如果
x 是 N 的因子,则 N/x 也是 N 的因子,只需要遍历 1 到 √N 即可找到所有因子。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt(); // 读取整数 N
sc.close();
List<Integer> factors = new ArrayList<>();
for (int i = 1; i * i <= n; i++) {
if (n % i == 0) {
factors.add(i); // i 是因子
if (i != n / i) {
factors.add(n / i); // N / i 也是因子
}
}
}
// 因子排序(如果需要从小到大排列)
Collections.sort(factors);
System.out.println(factors);
}
}
|
示例:
1
2
|
输入: 36
输出: [1, 2, 3, 4, 6, 9, 12, 18, 36]
|
时间复杂度:O(√N),相比 O(N) 的暴力方法,速度快很多!
2. 只判断因子个数(不存储)
如果你只想知道 因子个数,可以用计数器:
1
2
3
4
5
6
7
8
|
int count = 0;
for (int i = 1; i * i <= n; i++) {
if (n % i == 0) {
count++;
if (i != n / i) count++; // 计数因子
}
}
System.out.println(count);
|
示例:
3. 特殊优化:只找素因子
如果你只想找 素数因子(即 N 被哪些素数整除),可以用试除法:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
public static List<Integer> primeFactors(int n) {
List<Integer> primes = new ArrayList<>();
// 先除去 2
while (n % 2 == 0) {
primes.add(2);
n /= 2;
}
// 再检查奇数
for (int i = 3; i * i <= n; i += 2) {
while (n % i == 0) {
primes.add(i);
n /= i;
}
}
// 如果剩余的是素数
if (n > 1) primes.add(n);
return primes;
}
|
示例:
1
2
|
输入: 36
输出: [2, 2, 3, 3] // 36 = 2² × 3²
|
时间复杂度:O(√N),比 O(N) 方法快很多。
总结
| 方法 |
适用场景 |
复杂度 |
备注 |
| O(√N) 遍历因子 |
找出所有因子 |
O(√N) |
推荐 |
| O(√N) 计数因子 |
只求因子个数 |
O(√N) |
无需存储 |
| 试除法找素因子 |
仅找素因子 |
O(√N) |
用于分解质因数 |
如果只是找因子,推荐 O(√N) 方法,速度快,代码简洁! 🚀
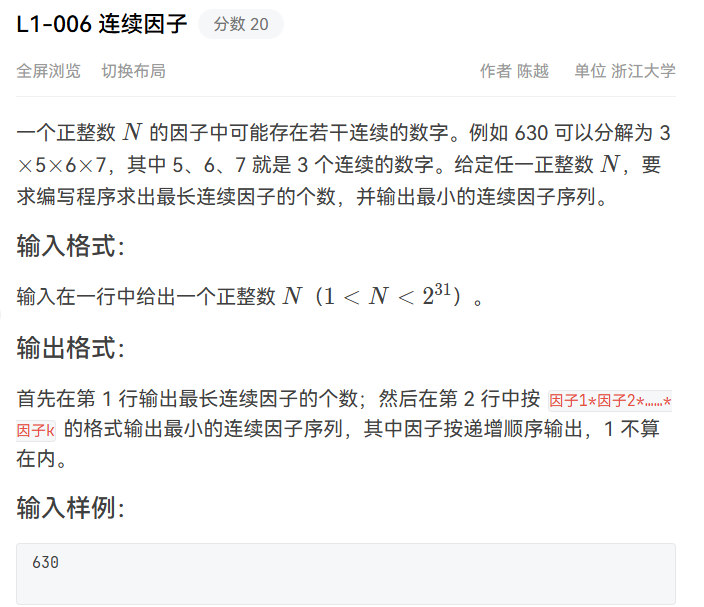
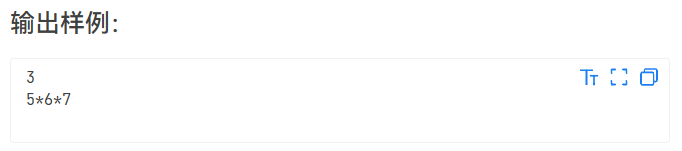
例题:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
|
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
long n = sc.nextLong(); // 读取 N,注意这里用 long,防止溢出
sc.close();
int maxLen = 0; // 记录最长长度
int start = 0; // 记录最长序列的起始因子
// 遍历起始因子 i,从 2 开始(1 不算)
for (int i = 2; i * i <= n; i++) {
long product = 1;
int j = i;
// 计算连续乘积,直到超出 N
while (product * j <= n) {
product *= j;
// 如果这个连续乘积刚好整除 N
if (n % product == 0) {
int length = j - i + 1; // 计算当前序列的长度
if (length > maxLen) {
maxLen = length;
start = i;
}
}
j++; // 继续尝试下一个连续因子
}
}
// 如果没有找到合适的连续因子,最长序列就是 N 本身
if (maxLen == 0) {
System.out.println(1);
System.out.println(n);
} else {
System.out.println(maxLen);
for (int i = 0; i < maxLen; i++) {
if (i > 0) System.out.print("*");
System.out.print(start + i);
}
}
}
}
|